Emmanuel Fromager and co. published a new paper, “Unitary transformations within density matrix embedding approaches: A perspective on the self-consistent scheme for electronic structure calculation“, in Physical Review B : 10.1103/PhysRevB.108.155119
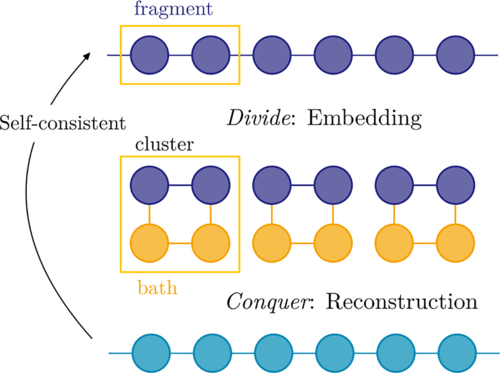
In this work, we introduce a self-consistent scheme based on the one-body reduced density matrix (γ) formalism. A significant feature of this methodology is the utilization of an optimal unitary transformation of the Hamiltonian, determined through a self-consistently determined, unitary reflection R[γ]. This enables the extraction of all reduced properties of the system from a smaller, accurately solved embedding cluster, and the systematic reconstruction of the reduced density matrix of the system. This process ensures that both extended and embedded systems satisfy the local virial-like relation, providing quantitative insight into the correspondence between the fragment in the extended system and its embedded analog. The performance and convergence of the method, as well as the N-representability of the resulting correlated density matrix, are evaluated and discussed within the context of the one-dimensional Hubbard model, which provides exact results for a comprehensive comparison.